SYCL Tutorial 3: Integrating SYCL Into Stanford University Unstructured
05 November 2014
Articles in this series
- Tutorial 1: The Vector Addition
- Tutorial 2: The Vector Addition Re-visited
- Tutorial 3: Integrating SYCL Into Stanford University Unstructured
1 Introduction
In part 3 of the SYCL™ tutorial series, we will look into integrating SYCL into a larger existing application. For this example, we have chosen to look into the Computational Fluid Dynamics (CFD) application Stanford University Unstructured .
2 Stanford University Unstructured
Stanford University Unstructured (SU2) is a scientific set of tools to do Partial Differential Equation (PDE) analysis and to solve PDE-constrained optimization problems. The software package is mainly focused on solving CFD-related problems. While fluid dynamics have many use cases, one of the more interesting applications is in aerodynamics. Here, the movement of air around a solid object, such as an aeroplane, is studied. Aerodynamics are also used in other fields, such as car manufacturing (including heavy use in the design of race cars, for example Formula One), and even in designing hard drives.
SU2 is developed by the Aerospace Design Laboratory (ADL) at Stanford University, but is Open Sourced under GNU Lesser General Public License Version 2.1. The full source can be found on GitHub.
At the heart of solving fluid dynamic problems are the Navier–Stokes equations. However, SU2 also supports other solvers such as Euler and Reynolds-Averaged Navier-Stokes. Simulation of the fluid dynamics, that is, solving the PDEs, is done using an iterative solution method. Solving these also requires solving a system of linear equations.
To run SU2 you need two components. One is the “mesh” file. This file describes the solid object that you are interested in analysing. For example, this could represent an aeroplane wing. The second file is a configuration file describing both physical settings and settings about the solvers, such as max iterations.
Currently SU2 supports parallelization using MPI. It does so using a separate domain decomposition application that splits up the mesh into several distinct problems. Hereafter, the normal SU2 binary is run with the newly separated input files using MPI. These steps are usually combined by running an included python script. Several MPI API calls are used during execution to synchronize the computation across the different MPI instances.
SU2 is a command line application and has no graphical user interface. However, the results of the simulations can be viewed in several post-processing applications, both Open Source (Paraview) and Proprietary (Tecplot).

Simulation of the Inviscid ONERA M6 wing test case showing Mach numbers in the post processing software Paraview
3 Integrating SYCL
When integrating SYCL into an existing application, a good place to start is to analyze where it makes most sense to introduce the parallel computation. In SU2 there is already a parallel computational structure in place, so we will take a look at this first. As mentioned in the previous section, SU2 uses MPI to do data decomposition, before running the full computation on a smaller dataset. This is a method which is well suited for distributed memory architectures, however, in the context of SYCL, doing parallelization this way imposes several issues with the current design of SU2. For example, there are several instances of recursion, class structures containing pointers, and use of dynamic memory, all of which are not allowed in SYCL. While it may be possible to do parallelization this way in SYCL, it would require a major re-write of the software to eliminate the aforementioned problems. Another point to consider is that re-writing the code into doing a similar parallelization as the current MPI solution would inevitably break the MPI support. If possible, it would be great to maintain the MPI support and as a result make it possible to run the code on a distributed GPU cluster.
Taking the above into account leaves us with many different places to introduce SYCL accelerated code; for example matrix operations would be a likely candidate. However, there is also a linear solver, with several preconditioners that should be well suited. A preconditioner is an operation on the data that makes it more suited for numerical applications and algorithms, and in turn improves the convergence of the linear solver. There is also a setup phase that might be able to be accelerated. To get a good speedup, more than one thing should be accelerated using SYCL.
In this example we will look at the matrix vector product, a function heavily used by the linear solver in SU2. An example of a matrix vector product (AB) is shown below. It is equivalent to a normal matrix multiplication where matrix A is multiplied by matrix B where B has one column and the same number of rows as the number of columns in matrix A.
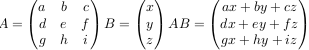
In SU2, the matrix vector product is located in the library “Common”, which is shared between all the software modules of SU2. To be exact, the source of all matrix operations, including the matrix vector product, is in the file Common/src/matrix_structure.cpp, and the header file is located in Common/include/matrix_structure.hpp.
The following is the original code of the matrix vector product routine from the 3.2.0 version of SU2.
void CSysMatrix::MatrixVectorProduct(const CSysVector & vec, CSysVector & prod, CGeometry *geometry, CConfig *config) {
unsigned long prod_begin, vec_begin, mat_begin, index, iVar, jVar, row_i;
/*--- Some checks for consistency between CSysMatrix and the CSysVectors ---*/
if ( (nVar != vec.GetNVar()) || (nVar != prod.GetNVar()) ) {
cerr << "CSysMatrix::MatrixVectorProduct(const CSysVector&, CSysVector): "
<< "nVar values incompatible." << endl;
throw(-1);
}
if ( (nPoint != vec.GetNBlk()) || (nPoint != prod.GetNBlk()) ) {
cerr << "CSysMatrix::MatrixVectorProduct(const CSysVector&, CSysVector): "
<< "nPoint and nBlk values incompatible." << endl;
throw(-1);
}
prod = 0.0; // set all entries of prod to zero
for (row_i = 0; row_i < this->nPointDomain; row_i++) {
prod_begin = row_i*this->nVar; // offset to beginning of block row_i
for (index = this->row_ptr[row_i]; index < this->row_ptr[row_i+1]; index++) {
vec_begin = this->col_ind[index]*this->nVar; // offset to beginning of block col_ind[index]
mat_begin = (index*this->nVar*this->nVar); // offset to beginning of matrix block[row_i][col_ind[indx]]
for (iVar = 0; iVar < this->nVar; iVar++) {
for (jVar = 0; jVar nVar; jVar++) {
this->prod[(const unsigned int)(prod_begin+iVar)] += this->matrix[(const unsigned int)(mat_begin+iVar*nVar+jVar)]*this->vec[(const unsigned int)(vec_begin+jVar)];
}
}
}
}
/*--- MPI Parallelization ---*/
SendReceive_Solution(prod, geometry, config);
}
Note that the code here is slightly modified to show class members more clearly.
In the above code, we multiply a given CSysMatrix object with the CSysVector object passed in as a parameter to the function. The result is stored in the CSysVector prod variable, which is likewise passed to the CSysMatrix member function.
The code might seem to be fairly complicated, keeping in mind the mathematical formula for the matrix vector product. The reason for this is that we are dealing with a sparse matrix, that is, a matrix with a large number of zero-values. To optimize the algorithm, the developers of SU2 have chosen to use the Block Compressed Row Storage format, which is a modification of the more widely used Compressed Row Storage format. This complicates the code a little, but improves the execution time. The storage format, and associated algorithm, skips access to, and storage of, as many zero-values as possible. Information about row and column indexes is stored in the row_ptr and col_ind arrays.
There have been several papers and much research into optimizing sparse matrix multiplication on GPU devices. While the block format is likely better than the normal Compressed Row Storage variant, there may be better solutions. Some research into this area has been done by Nvidia in their technical report "Efficient Sparse Matrix-Vector Multiplication on CUDA".
Creating a SYCL version of the algorithm used in SU2 should be relatively straightforward bearing in mind what we have learned in the previous SYCL tutorials. The full code for the SYCL version is shown below.
void CSysMatrix::MatrixVectorProduct(const CSysVector & vec, CSysVector & prod, CGeometry *geometry, CConfig *config) {
unsigned long prod_begin, vec_begin, mat_begin, index, iVar, jVar, row_i;
/*--- Some checks for consistency between CSysMatrix and the CSysVectors ---*/
if ( (nVar != vec.GetNVar()) || (nVar != prod.GetNVar()) ) {
cerr << "CSysMatrix::MatrixVectorProduct(const CSysVector&, CSysVector): "
<< "nVar values incompatible." << endl;
throw(-1);
}
if ( (nPoint != vec.GetNBlk()) || (nPoint != prod.GetNBlk()) ) {
cerr << "CSysMatrix::MatrixVectorProduct(const CSysVector&, CSysVector): "
<< "nPoint and nBlk values incompatible." << endl; throw(-1); } prod = 0.0; // set all entries of prod to zero double *vec_ptr = vec.GetData(); double *prod_ptr = prod.GetData(); unsigned long nvar = this->nVar;
{ // sycl scope start
default_selector selector;
queue myQueue(selector);
cl::sycl::buffer<double, 1> buf_vec(vec_ptr, vec.GetSize());
cl::sycl::buffer<double, 1> buf_prod(prod_ptr, prod.GetSize());
cl::sycl::buffer<double, 1> buf_matrix(this->matrix, nnz * nVar * nEqn);
cl::sycl::buffer buf_row_ptr(this->row_ptr, nPoint+1);
cl::sycl::buffer buf_col_ind(this->col_ind, nnz);
command_group(myQueue, [&]() {
auto acc_vec = buf_vec.get_access();
auto acc_prod = buf_prod.get_access();
auto acc_matrix = buf_matrix.get_access();
auto acc_row_ptr = buf_row_ptr.get_access();
auto acc_col_ind = buf_col_ind.get_access();
auto myRange = nd_range(range(nPointDomain));
auto myKernel = ( [=](item<1> item) {
unsigned long prod_begin, vec_begin, mat_begin, index, iVar, jVar;
int row_i = item.get_global();
prod_begin = row_i*nvar; // offset to beginning of block row_i
for (index = acc_row_ptr[row_i]; index < acc_row_ptr[row_i+1];
index++) {
vec_begin = acc_col_ind[index]*nvar; // offset to beginning of block col_ind[index]
mat_begin = (index*nvar*nvar); // offset to beginning of matrix block[row_i][col_ind[indx]]
for (iVar = 0; iVar < nvar; iVar++) {
for (jVar = 0; jVar < nvar; jVar++) {
acc_prod[(const unsigned int)(prod_begin+iVar)] +=
acc_matrix[(const unsigned int)(mat_begin+iVar*nvar+jVar)]*
acc_vec[(const unsigned int)(vec_begin+jVar)];
}
}
}
});// kernel end
parallel_for(myRange,
kernel_lambda(myKernel));
}); // command group end
} // sycl scope end
/*--- MPI Parallelization ---*/
SendReceive_Solution(prod, geometry, config);
}
As in our previous tutorials, the first steps in our SYCL-ported code are to choose an OpenCL™ device and create a queue. In SYCL, we can use one of several predefined device selectors. In this example, we have used the default_selector , which means that the implementation-specific SYCL runtime will select the OpenCL device that it finds most suitable. Following this, we can create a queue for the device.
We now need to set up buffers for the data needed when executing the kernel. Note that, in this function, we are dealing with custom classes to hold the vector and result (CSysVector). Internally, this class stores the data as a dynamic array of doubles. While this makes it impossible to use directly with a SYCL buffer, a simple getter function to the internal representation of the object makes this possible. Therefore, we have introduced a GetData getter method in the CSysVector class. In this example, we need to use class variable nVar in our kernel. It is not possible to capture a class member variable by value in a C++ 11 lambda. It is only possible to capture a pointer to this, however copying a pointer to an OpenCL device is undefined. As a result, we copy the class member variable into a local scoped variable, which can be captured by the lambda. Furthermore, we note that some of the data used here is of type double. Hence, an OpenCL device that supports the optional double type is required in order to run the above code.
Following the creation of the buffers, we create a command group, inside of which we can enqueue data and our kernel to the device. Inside the command group, we first create the accessor to our buffers. Note that, in our kernel, we only need to write to the result vector prod, whereas the remaining data only requires read access. We can now define our workgroup size, using the nd_range object. In this case, we want the workgroup size to be nPointDomain, to introduce the parallelism on the most outer loop of the original implementation. One thing to keep in mind, however, is that the nPointDomain may not match well to the OpenCL device’s preferred workgroup multiple, and we may therefore want to change the number slightly for optimizations. We have chosen to let the local workgroup size be undefined, and let the SYCL implementation choose a value for us. The kernel is now specified. The code in the kernel is identical to the original solution, with the outermost loop removed, and variable names changed to use the created SYCL assessors and the local nvar variable, which is being captured by the lambda. No further changes are needed to the original algorithm.
Now we can launch the kernel using the parallel_for call with our defined kernel and range objects.
4 Conclusion
In this tutorial, we have shown how SYCL can be integrated into a large scale scientific application, with minimal code and structural changes. In the ported code, we have added support for parallelization using OpenCL-compatible devices by adding less than 30 lines of additional code to the original software. Furthermore, we have shown how SYCL can compliment other forms of parallelization, by retaining the original MPI support of SU2, making it possible to execute the application on a GPU cluster. This makes the code highly scalable and suitable to solve very large and computationally heavy simulations that are required in the field of fluid dynamics.
You can learn much more about SU2 on their website and in their two published papers below.
5 Disclaimer
Please, note that the above code is based on the provisional specification of SYCL. The final specification is subject to change from the current draft.
The code in this blog post is licensed under GNU Lesser General Public License version 2.1 which can be found in full here: http://www.gnu.org/licenses/lgpl-2.1.html.
The full code for SU2 can be found directly on GitHub: https://github.com/su2code/SU2.
Khronos and SYCL are trademarks of the Khronos Group Inc.
OpenCL and the OpenCL logo are trademarks of Apple Inc. used by permission by Khronos.
